De afronding op 5 cent of wanneer de overheid Don Quichotte komt spelen in uw verkooppunt

Terug naar de weblog

21/01/2019

Hier zijn we dan, de dag na de inwerkingtreding van de verplichting van afronding op 5 cent ...

Bijna 18 jaar na de invoering van de euro, onze monetaire autoriteiten hebben eindelijk begrepen dat de munten van 1 en 2 cent enkel nadelen hadden: duur om te produceren, duur om te beheren, duur (voor de winkeliers) om naar de bank te gaan... We kunnen ons vandaag afvragen of het oorspronkelijk in omloop brengen van deze stukken zeer relevant was. Maar ja, dat is het verleden.

Vandaag, horen onze leiders de doodsklok van het gebruik van die onbeduidende stukjes koper. Oké. Een eerste poging in 2014 op vrijwillige basis gaf weinig resultaat. Zo begint de "dwingende" fase. Het is tijd om de regelgeving in een keurslijf te plaatsen. Voldoende aangespannen, zodat het ministerie van Economische Zaken om de 3 dagen moest veranderen de referentie pagina.

Laten we eraan herinneren dat we gingen van een aanbeveling:

1 verkoop = 1 betaalwijze = 1 enkele afronding op het totaal van de verkoop

Naar deze aanbeveling :

Vóór elke betaling, vraag eerst uw klant het bedrag dat hij wil betalen met behulp van een betaalmiddel waarvan het bedrag is vastgesteld of opgelegd (zoals maaltijdcheques, eco-cheques, cadeaubonnen, etc.). Zodra dit bedrag is betaald, gelden de beginselen van de afronding op het saldo van het oorspronkelijke bedrag dat cash wordt betaald.

En een sectie "veel gestelde vragen" die voor onbeperkt uitstrekt.

Kleine quiz

Een leverancier van pizza’s komt bij jou en vraagt om 24,36 € voor de Quatro Stagione en de Margerita die hij levert. Hij heeft een draagbare betaalterminal, maar jij kiest voor een cash betaling. Moet hij afronden ?

Denk na… Het antwoord is te vinden in het artikel VI.7/1 en VI.7/2 van Wetboek van Economisch Recht.

livreur - chauffeur - la question de l'arrondi

Verrassend, als wij winkeliers en consumenten ondervragen, dan is iedereen ervan overtuigd dat hij zal verliezen. Een mooie unanimiteit, echter, onthult een diepe inconsistentie en een gebrek aan begrip van de toegepaste afronding. Doe een moeite aub….

De bedragen die eindigen op 1, 2, 6 en 7 worden naar onder afgerond. Degenen die eindigen op 3, 4, 8, 9 naar boven afgerond. Daarom zullen er evenveel afronding naar onder als naar boven zijn, zodat niemand wint en niemand verliest.
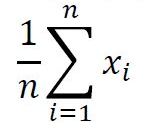
formule arrondi

Om dit te begrijpen, hebben we de oefening gemaakt door 1.300.000 tickets die wij in Mercator gegevens van sommige van onze klanten hebben gevonden, te verzamelen .

We berekenden de voorgeschreven afronding en berekenden het verschil tussen het "natuurlijke" bedrag en het "afgerond" bedrag. Het gemiddelde van dit verschil bedraagt 0,0015529657682533441. Dus op basis van een dergelijke monster, opdat een klant 1 € zou verliezen, dan zouden er 837.107.956 tickets nodig zijn.

Afgezien van deze economisch onbeduidende problematiek in kwestie, wordt de vraag gesteld of het imago dat de wetgever heeft bij zijn hardwerkende winkeliers, die de economie van het huis België doen draaien en die zelf nooit in "lopende zaken" zijn.

Hij heeft een berekeningsalgoritme bepaald: het is voor iedereen duidelijk. Dankjewel ! Maar al deze eisen en aanvullende voorwaarden, die in de praktijk tegen zo veel verstrikkingen en smerige hindernissen bij het uitvoeren van de handel verschijnen, waren deze echt nodig?
De “handelaar”, is hij de grote boze wolf die elke klant met zijn knuppel opwacht om zijn munten te stelen van een en twee cent.

Droevige visie …

Deze strijd van onze leiders tegen hun eigen economie is volledig nutteloos.

En nu, onze kleine quiz?

Ja? Non? Niet eenvoudig!

Als diegene die levert ook de verkoper is, dan is de verplichte afronding van toepassing als je cash betaalt, want je bent “in de gelijktijdige fysieke aanwezigheid van de consument en de onderneming”. Maar, als diegene die levert een tussenpersoon die enkel de pizza’s levert is, dan is de afronding niet van toepassing.